anovat and anovap functions in the Factory
The anova functions verify that a certain quantitative variable (dependent variable) keeps the same stochastic distribution against the clusters which have been led by a nominal variable (independent variable).
The null hypothesis states that when when the independent variable varies, the dependent variables' distribution doesn’t change, whereas the alternative hypothesis is the consequence of the null hypothesis' refusal, which means that the dependent variables' distribution varies when the independent variable changes.
anovat() returns the ANOVA test value.
anovap() returns the p value, that is the probability to obtain a worst case compared to the null hypothesis we are verifying. Values above 0.05 (i.e. the conventional value for alpha) state that we can’t reject the null hypothesis, while values below 0.05 state that we need to reject the null hypothesis and consider the alternative one.
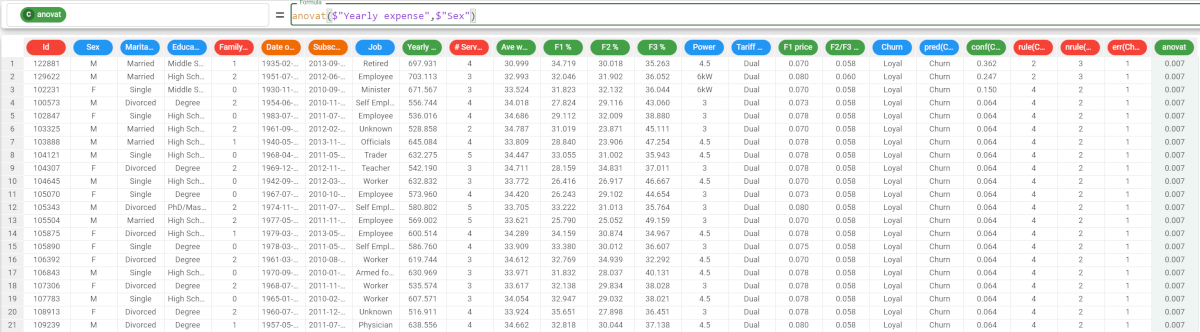
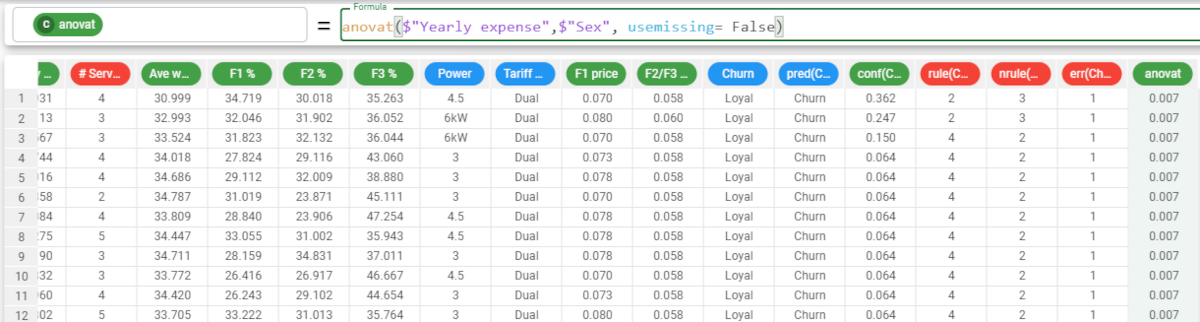
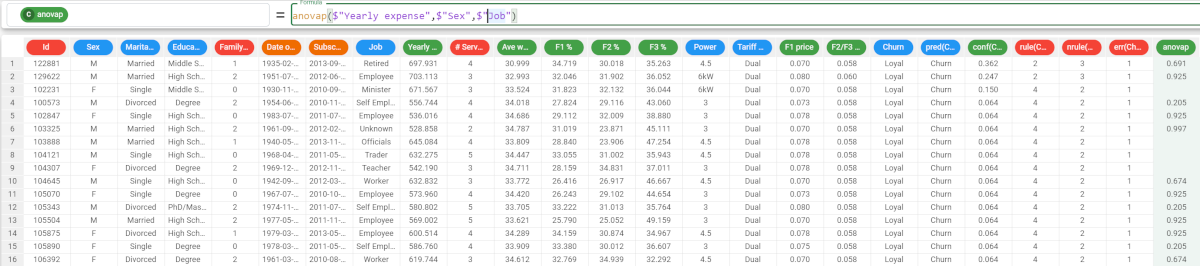
Parameters for anovat and anovap Parameter Description column1 The continuous attribute used to evaluate the ANOVA p or t value. The column1 parameter is mandatory. attclass The nominal attribute used to evaluate the ANOVA p or t value. If it is not nominal, it will be casted to nominal upon function’s computation. The attclass parameter is mandatory. group The attribute by which group results. More than one column can be specified in this parameter, as long as all attributes are enclosed in double brackets. usemissing A Boolean which indicates whether missing values should be considered or not in the computation of the statistics. The default value, if not otherwise specified, is True. Example - anova t The following example uses the make single offer tariff order dataset. Description Screenshot In this example, we want to retrieve the anovat value of the Yearly expense attribute. The formula to write is: In this example, we have decided to not include any missing values in the calculations, so we want to set the usemissing parameter to false. As we have not specified a group parameter, we cannot use the position of the parameter to identify it, so we must use the keyword of the parameter to identify its meaning. So the consequent formula would be Example - anova p Description Screenshot In this example, we want to retrieve the anovap value using the same attributes as in the example above. The formula to write is: If we want to be more precise with the analysis, we can add the group parameter, as we want our results to be grouped by the Job attribute. The formula to write is: The results are as follows: The p value of the Retired people is 0.691; The p value for the Employees is 0.925, and so on. As the alpha value is 0.05, we can’t reject the null hypothesis considering the Retired group (i.e. a value of the Job attribute), so the Yearly expense for the males and the females (i.e. the values of the Sex attribute, the independent variable) follows the same stochastic distribution. anovat(column, attclass, group, usemissing)anovap(column, attclass, group, usemissing)anovat($"Yearly expense",$"Sex")anovat($"Yearly expense",$"Sex", usemissing = False)anovap($"Yearly expense",$"Sex")anovap($"Yearly expense",$"Sex",$"Job")