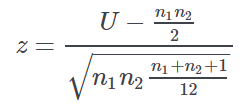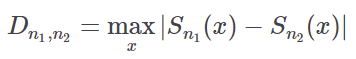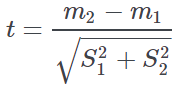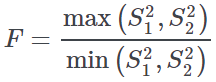Sample size

Number of valid positive, negative and total samples

The number of valid samples for both attributes n is displayed, for positive, negative and total data samples respectively.

This is particularly useful when there is a heavily unbalanced distribution of missing data among the two attributes, which might cause the analysis to be based on an unacceptably small sample size.

Wilcoxon and Mann-Whitney test

• Mann-Whitney U-value 

• Mann-Whitney normalized U-value

• Wilcoxon R₁-value

• Wilcoxon Normalized R₁-value

The non-parametric test of Mann-Whitney and the Wilcoxon equivalent variant are both available.

Items include U-value, which represents the number of couples of subjects selected by the two groups among which the continuous attribute shows the highest value in the target group. In the U calculation, couples with equal values contribute with 0.5 each. 

The Normalized U-value is the corresponding proportion of couples, thus representing an estimate of the probability of correctly ranking two subjects randomly selected from the two groups. Normalized U-value is the equivalent to the AUC area under the ROC curve obtained by the two selected attributes. 

R₁-value is the lowest value of the rank sum, calculated inside the two groups. It frequently, but not necessarily, corresponds to the sum of ranks inside the smallest group. R₁ is also known as the Wilcoxon statistic test and is easily obtained by the following procedure:

1. Pool together the values of the continuous attributes of the two groups you are comparing

2. Transform each value into the corresponding rank

3. Separate the ranked values by group

4. Calculate the sum of the ranks in the two groups and take the lowest R₁ value.

Under the null hypothesis of an equal distribution of the continuous attribute inside the two groups, the two corresponding rank sums will be similar, then a very low value of R₁ will correspond to a high probability of an actual difference between the two distributions. In the absence of coincident values (ties) the Mann-Whitney test and the Wilcoxon test are equivalent to assess the difference between the median values among the two classes. The test is very powerful in the presence of a “shift” model, i.e. when the two groups share distributions that differ only by a constant value. Conversely, the test in general is unable to identify small local differences between the two distributions (the Kolmogorv-Smirnov test could be applied instead).

The equivalence between the Mann-Whitney test and the method proposed by Wilcoxon relies on the fact that U is a simple linear transformation of R₁:

where n₁ and n₂ represent the sample size of the two groups. The corresponding p-value is obtained by assuming an asymptotic Normal distribution for the U statistic:

where z follows a Normal standard distribution.

Kolmogorov-Smirnov test

KS Value and P-value for KS test

A non-parametric tool for comparing a continuous distribution between two groups.

Similarly to the Wilcoxon-Mann-Whitney approach it tests the null hypothesis that the two distributions are equal, looking for any difference inside the two empirical distributions. In particular, in the presence of local differences it tends to be more powerful than the Mann-Whitney test, whereas when the continuous attribute has a similar distribution among the two groups, but with different median values, the former approach is uniformly more powerful.

The Kolmogorov-Smirnov test is based on the maximum absolute difference between the two empirical distributions S_n1 and S_n2 of the values of continuous attribute inside the two groups:

The corresponding p-value is obtained by the exact cumulative null distribution of n₁n₂D_n1,n2. The Kolmogorv-Smirnov statistic D_n1,n2 has an interesting relationship with the ROC curve obtained from the same two attributes, as it corresponds to the highest vertical distance between the curve and the rising diagonal, also corresponding to the highest value of the Youden index.

Student t-test

Student t-value and P-value for Student t-test

The most popular statistical test for comparing two classes.

It is used to assess the null hypothesis that the mean values of the distribution of the continuous attribute inside the two groups are not different. It lies on the assumption that the continuous variable is normally distributed inside each group.

The test is available in two different versions. The first default test assumes that the continuous variable has the same variance in the two groups:

where m₁ and m₂ represent the means of the two groups, S₁ and S₂ the corresponding variance estimates and n₁ and n₂ the number of valid data in each group. The expression inside the square root at the denominator of the equation is usually called “the estimate of the pooled variance”.

The Student t test for unequal variances is obtained by the following equation:

In both cases the inference (i.e. the p-value calculation) is made by assuming that t follows a Student t distribution with n₁+n₂−2 degrees of freedom. Such an assumption is met when the two samples are independent and the distribution of the continuous attribute within each group is Normal (Gaussian).

Levene test

F-value for Levene test and P-value for Levene test 

This test is used to compare the variance of the continuous attribute between two groups, using the following equation:

F follows a Fisher F distribution when the two variances are actually equal (i.e. under the null hypothesis) and if there is a Normal distribution of the attribute inside the two groups. The degrees of freedom for the numerator and the denominator corresponds to n₂−1 and n₁−1 respectively, if s²₂ > s²₁.

If however s²₁ <= s²₂ the degrees of freedom for the numerator and the denominator instead correspond to n₁-1 and n₂-1, respectively.

Parameters

Use target attribute

Selecting target value for … it is possible to choose the target value for each statistical analysis.

If the target attribute is dichotomic, the selection will have an effect on the Student t test only, changing the sign of the t statistic; because the corresponding p-value is evaluated for two sided tests, it will remain unchanged.

Student t-test parameters

Options

The type of Student t test. 

Possible types are:

• use equal variance

• use unequal variances

• use automatic selection. This is the default selection, and performs the Levene test to assess the hypothesis of equal variances and, accordingly, automatically choose the more suitable variant.