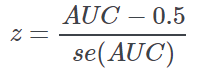Computing ROC Curves in the Sheets tab
The ROC curve compares the distribution of a continuous attribute between two separate groups defined by a binary attribute (or compares the distribution of two continuous attributes), using standard ROC analysis tools. ROC analysis is the statistical analysis of ROC curves.
Rulex provides simple bivariate plots that show the relationship between true positive (sensitivity) and false positive (1-specificity) results obtained by a set of binary classification tests. The set of binary tests is obtained using each value of the continuous attribute as a threshold and test positivity is defined by values higher than the threshold, as is the norm in standard ROC analysis.
There are two different types of ROC curve statistics:
scalar, which refer to the main ROC curve parameter, the Area Under Curve (AUC) and some related statistics. If the ROC curve is a concave and symmetric curve the point criteria will have the same cut-off, apart form the Point of maximum accuracy, which depends on the sample size in the two groups under study.
vector, where the ROC table corresponding to the ROC curve is obtained.
Properties | Description |
|---|---|
General parameters | |
Statistics on integer variables are continuous | If selected, statistics will be displayed as continuous values. Rulex provides the possibility to force some output, such as the values of ROC cut-offs, or to provide integer values. The former option can be applied only to original (non-transformed) data, thus it has no effect when applied to test statistics and their related p-values. |
Sample size | |
Number of valid positive samples | The number of valid positive data samples for both attributes n is displayed. A data sample is positive when its target is positive. |
Number of valid negative samples | The number of valid negative data samples for both attributes n is displayed. A data sample is negative when its target is negative. |
Number of total valid samples | The number of valid data samples for both attributes n is displayed, and corresponds to the total of the number of valid positive and negative samples. This is particularly useful when there is a heavily unbalanced distribution of missing data among the two attributes, which might cause the analysis to be based on an unacceptably small sample size. |
Roc Curve (scalar) | |
Area under curve | The area under the ROC curve measures the accuracy, whereby 1 is a perfect test, and .5 a worthless test. |
p-value of AUC and Standard error of AUC | The p-value is obtained exploiting the asymptotic normal distribution of AUC: where se(AUC) is the standard error of AUC obtained. The numerator in the equation above represents the difference between AUC and 0.5, its expected value under the null hypothesis of an equal distribution of the continuous attribute among the two classes under study. |
Point of maximum youden index | A popular measure of test accuracy obtained as the sum of sensitivity and specificity minus 1, which corresponds to the point of the ROC curve with the highest vertical distance from the rising diagonal. |
Point closest to (0,1) | The left top point in the ROC plot, which corresponds to the maximum possible accuracy (100% of samples correctly classified). |
Point of maximum accuracy | The empirical observed cut-off, which allows the highest proportion of correct classifications. |
Point with specificity = sensitivity | The point at which the accuracy is the same for negative and positive cases |
Rc Curve (vector) | |
AUC 95% confidence interval | If selected, the minimum and maximum AUC 95% confidence interval is calculated and displayed. The standard error of the AUC, used to calculate the confidence interval, is computed using the method selected in the Standard error of AUC computation method option. |
1-specificity | The y coordinates of the ROC curve. |
Sensitivity | The x coordinates of the ROC curve. |
Accuracies | The quota of correct predictions. |
Thresholds | The corresponding cut-off, obtained by interpolation of couples of consecutive original values of the continuous attribute |
Youden indices | Youden indices are indicators of balanced accuracy, expressed as specificity + sensitivity -1. |
Likelihood ratio - | The negative likelihood ratio, expressed as 1-sensitivity divided by specificity. |
Likelihood ratio + | The positive likelihood ratio, expressed as sensitivity divided by 1-specificity. |
Parameters | |
Use target attribute | If selected, statistics are computed on the values of the continuous attribute X, previously split into two groups defined by the dichotomic attribute Y. If Y is not dichotomic, it is possible to use a binarization criterium. The splitting criterion is set by clicking on target value(s) for and setting the required filter. A window is displayed where you can chose how to binarize the Y attribute and consequently how to split the continuous X attribute into two groups. Otherwise, if left unchecked, comparisons are performed between the attributes X and Y. |
Roc Curve Parameters | |
Positive test for: | Different criterion that can be used to define test positivity. Possible values are:
|
Standard error of AUC computation method: | Select the method with which you want to calculate the standard deviation of the AUC, used in the AUC 95% confidence interval. Possible methods are Mann Whitney, Hanley-McNeill or DeLong. |
Consider missing target values as negative outcomes | If selected all missing target values will be considered as negative. |