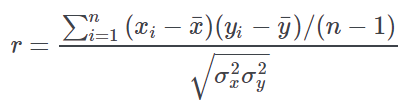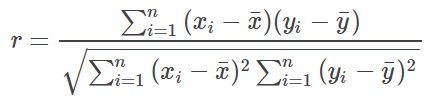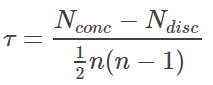Sample size

Number of total valid samples

The number of valid data samples for both attributes n is displayed.

This is particularly useful when there is a heavily unbalanced distribution of missing data among the two attributes, which might cause the analysis to be based on an unacceptably small sample size.

Pearson correlation coefficient

r-value for Pearson coeff.

The Pearson correlation coefficient is selected by default and is one of the most common measures of correlation between continuously distributed attributes.

The coefficient varies between -1 and +1 and takes negative values when there is a negative association, i.e. when high values of an attribute correspond (on average) to low values of the other attribute and vice versa. A value equal to +1 indicates a perfect association, which can be observed, for example, when the two attributes take the same values or if they just differ by a constant (e.g. X=Y+k). Conversely, a value =−1 indicates a perfect negative association. Finally, in the presence of two completely independent attributes, this coefficient takes a value close to zero.

The corresponding p-value is used to assess the (null) hypothesis that the correlation coefficient differs from the expected value of zero just by chance, thus indicating that there is no association between the two attributes.

The Pearson correlation coefficient measures the presence of a linear association between two attributes, which means that X is assumed to be either directly or indirectly proportional to Y. It means that a value close to zero does not necessarily imply that the two variables are not associated. For example, a quadratic relationship (e.g. X=Y²) could be present. A scatter plot of the two attributes can help to correctly interpret the observed correlation coefficient.

The Pearson correlation coefficient is estimated by the following equation:

Where o²x and o²y represent the variance of X and Y attributes, respectively, while the numerator of the above equation is called the “covariance” of X and Y.

Exploiting the relationship between variance and sample size this equation can also been expressed in the following way:

The Pearson correlation coefficient should be applied only to Normally (Gaussian) distributed variables. It is possible to check for the assumption of Normal distribution using the quantile-quantile plot, as explained in the Values, Frequencies and Quantiles in the Statistic Manager page.

The computation of the p-value for the Pearson correlation coefficient is obtained using the following formula:

where T follows a Student t distribution with n−2 degrees of freedom.

Spearman correlation coefficient

ρ-value for Spearman coeff.

The Spearman correlation coefficient is selected by default and is a widely used measure of pairwise association between continuously distributed attributes.

In the same way as the Pearson correlation coefficient, the Spearman correlation coefficient can vary between -1 and +1, taking negative values when there is a negative association, positive values when there is a positive association, and values close to zero for independent attributes.

This measure provides an alternative to the r-coefficient when there is a non-Normal (or simply unknown) distribution of either attribute and corresponds to the Pearson coefficient applied to the ranks of the values of the two attributes. Ranks are the progressive numbers of the ordered values of an attribute. 

The corresponding p-value is computed in the same way as the Pearson coefficient.

Kendall Tau

τ-value for Kendall Tau

The Kendall Tau is a correlation measure based on the ranks of the two attributes.

In its simplest version (sometimes called “the tau a”), for each row i the sign of X_i−Y_i is obtained. Then each row is compared with all the other rows, and the number of concordant (same sign) and discordant (different sign) couples is calculated.

The tau statistic (τ) is obtained as follows:

where n_disc and n_conc represent the number of concordant and discordant couples, respectively, while the denominator is the number of all possible couples. As a consequence, similarly to Pearson and Spearman correlations, tau values will range between -1 and 1 and they will be close to zero in the case of independence between the two variables (the null hypothesis). Rulex has implemented a variant of the tau statistic (sometimes called “the tau b”) that takes into account the possible occurrence of tied values, as an asymptotic normal test for the inference (i.e. for the p-value calculation).

Simple regression coefficient

β-value for Simple regression coefficient

The regression coefficient β₁ of the least square line, corresponding to the following regression model, is obtained:

The least square line can be displayed inside the corresponding scatter plot of Y vs X.

The corresponding p-value is obtained assuming that the ratio between the regression coefficient and its standard error follows a Student t test distribution with n−2 degrees of freedom.