parent

The attribute containing the parent nodes of a directed graph. The parent parameter is mandatory.

son

The attribute containing the son nodes of a directed graph. The son parameter is mandatory.

group

The attribute by which you want to further group results.

The group parameter can also be defined as a list: rootDistance($"parent",$"son",($"group1", $"group2"))

whichpath

When defined, it allows the user to choose which path is to be considered:

• the shortest one - whichpath = "minimum",

• the longest one - whichpath ="maximum" or

• all the paths - whichpath = "all" - in this case, distances are concatenated in a single string.

If no path is specified, the rootDistance function applies the “minimum” variable by default.

separator

It specifies the separator to use un the in the concatenation of different distances.

The default separator is "-"

This parameter can only be used when the whichpath = "all" is defined.

weights

The attribute defining the length of the edge.

operator

It defines how to combine weights attributes along the path to the root.

If left unspecified, the default operator applied is sum and the weight attributes will be summed. While if the operator is prod, they will be multiplied.

It can only be used if the weights parameter is specified.

In this example, we want to retrieve the distance of each node from the root of the directed graph.

This is a Bill of Material (BOM), and the parent-son relationship is defined respectively by the ParentComponentID and ComponentID attributes. As each row has not only information on the component itself, but also on its parent component, we can use the rootDistance function which calculates the distance of each component from the finished product.

We add a new attribute, and define the rootDistance function specifying which attribute is the parent and which is the son.

So, the formula is: rootDistance($"ParentComponentID",$"ComponentID")

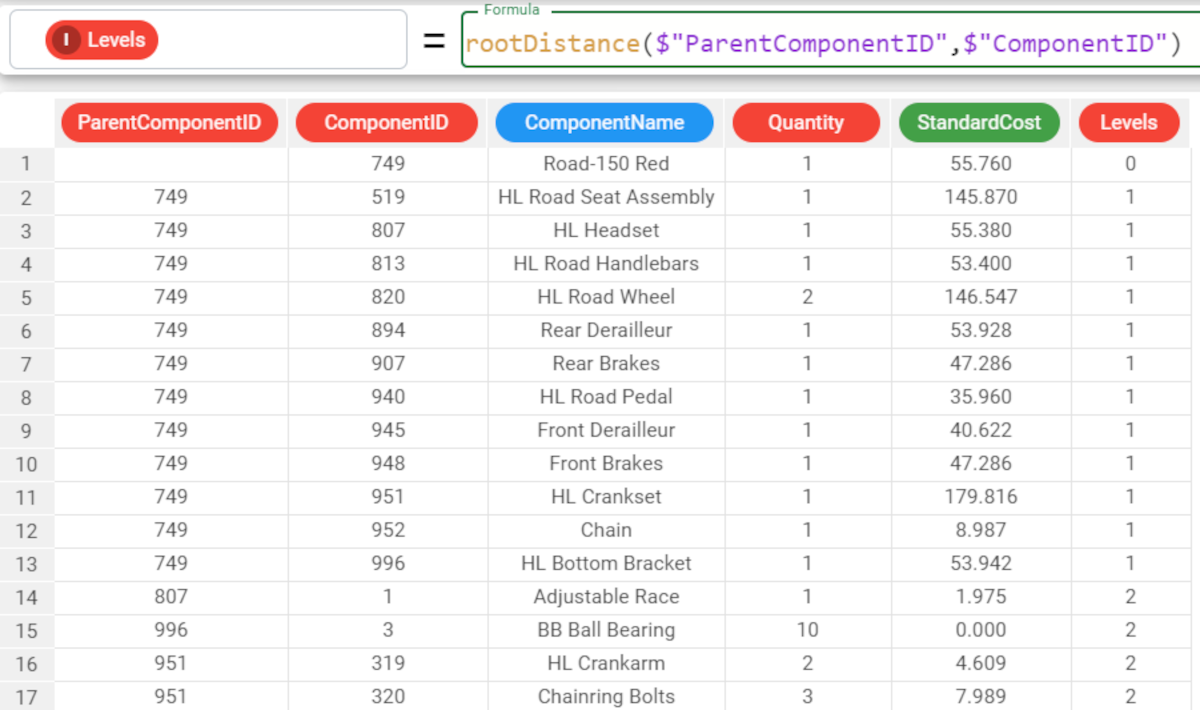
Here the rootDistance function has calculated how many parent levels each node has.

We can see that for the finished product in row 1, the parent level is 0 because we are already at the highest level of the hierarchy of the graph. While for the other components we can see all the intermediates levels up to 3, which is the maximum distance from the final product - root - of this directed graph.

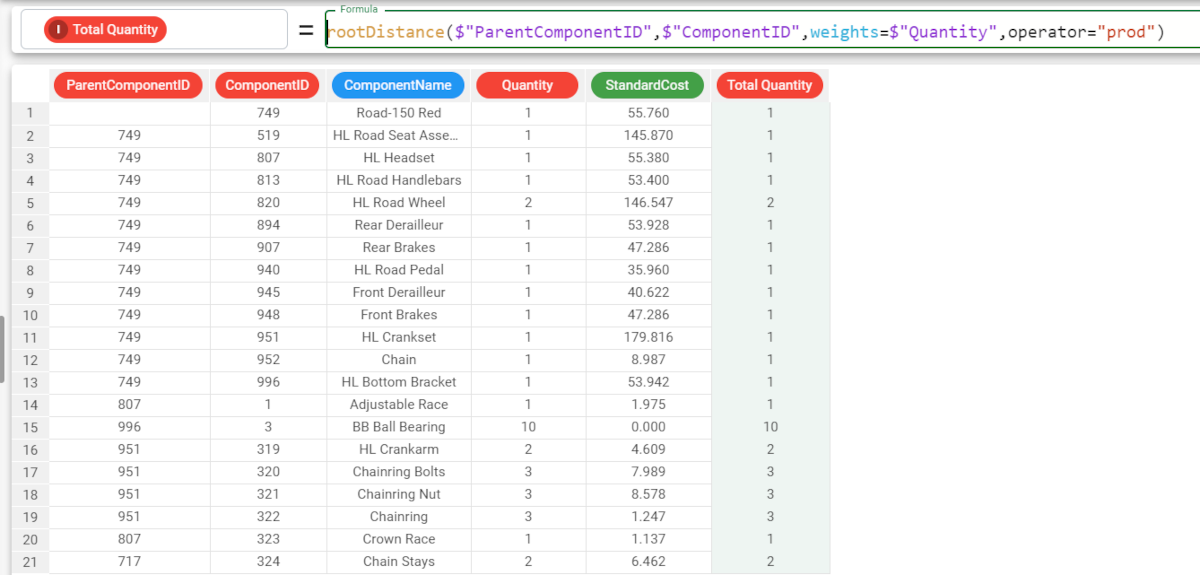
In this other example, we want to calculate the total quantity of component needed to build the final product.

The Quantity attribute states how many components we need to build the parent component, but not for the whole finished product.

To achieve this goal we need to define the rootDistance function as follows:

• specify which are the parent and son attributes,

• add the Quantity attribute as weights parameter as it defines the length of the edge,

• and specify the operator parameter as prod - which will multiply the results by the weight.

We add a new attribute and define the rootDistance function.

The consequent formula would be: rootDistance($"ParentComponentID", $"ComponentID", weights=$"Quantity", operator="prod")

In the picture we can see the results.